Situation

MCS Corporation produces an amazing toy called DinoBall. This toy is so popular that MCS Corporation can run 8 retail stores dedicated to selling just this product. MCS Corporation is dedicated to meeting all demand for Dinoball. The toy is produced at 3 production facilities owned by MCS Corporation, each of which has multiple production lines dedicated to producing the DinoBall toy. The characteristics of each of these production lines are a function of their age: newer production lines produce the DinoBall toy quicker and use less power. MCS Corporation plans monthly for production levels across its facilities based on the demand for DinoBall. Currently, DinoBall operates under the policy that each facility will, monthly, produce the same number of toys. In other words, the facilities are ‘balanced’ in that each of them produces 13 of DinoBall’s monthly demand. MCS Corporation likes the idea of equal ‘wear and tear’ on each production line at a particular facility: MCS Corporation currently implements the requirement that every production line at a facility runs for the same length of time during a month. For purposes of this analysis, you can assume that a ‘month’ consists of four 40 hour weeks (for a total of 160 hours). Each production line has the required salaried staff to operate the production lines who all work 40 hours per week. MCS Corporation contracts with LM Trucking to transport DinoBall from their facilities to their retail stores. LM Trucking needs your team to solve an optimization problem to determine the shipment levels and associated costs. The policy of LM Trucking is then to charge a premium of 20% to MCS corporation in billing them for the logistics services. MCS is charged for the energy they use to run their production lines. Due to their age, each production line requires different amounts of energy (kWh) and each production facility has negotiated a set price per kWh with the power company. MCS Corporation hired your group to address several areas of interest that they believe can be ad- dressed using Industrial and Systems Engineering models and methods. They provided you with past data (e.g., historical demand levels, distances between facilities and retail stores, characteristics of pro- duction lines) about their company to help address these areas of interest. The past data is available in the associated Excel file. The MCS Corporation is interested in addressing two ‘what-if’ questions independent of each other.

Question 1:

MCS Corporation is considering removing the policy that each facility is responsible for produc- ing the same number of toys. They believe that this would drive down their total operating costs but are concerned about the idea of restructuring their company (i.e., they may need to relocate workers amongst their facilities, increase worker hours). MCS Corporation is interested in deter- mining the amount of savings that would result from removing this policy. Note that the “even wear and tear” policy on the production lines will remain in place.

Question 2:

MCS Corporation has an opportunity to update all production lines with the new technology ‘FastProd’. This new production line will decrease production costs of DinoBall since FastProd produces at a faster rate with less energy. They believe that the life cycle of each new production line will be 3 years. The company that sells FastProd insists that they will only install FastProd at the facilities of MCS Corporation if all production lines are outfitted with FastProd. MCS plans to sell each existing production line that is replaced; however, MCS is unsure how much they will be able to sell the used lines for. MCS Corporation would like to determine a ‘reserve price,’ which is the maximum amount they are willing to pay for this type of contract, in preparing to negotiate with the company that produces FastProd.

Task

This project is about helping MCS Corporation to minimize their operating cost by optimizing their production and transportation process using linear programming with Gurobi. We provide three linear programming models to solve the following problems:

1. Original Model: What is the optimal quantity for each factory producing the same quantity?
2. ‘What If’ question 1 Model: What is the optimal quantity for each factory producing a different quantity?
3. ‘What If’ question 2 Model: What is the reserve price of the old production line if the company replaces the new production line?

After applying Gurobi, we will get the results related to the model, including units produced at each factory (decision variables), the minimum cost (the objective function) based on all the necessary limitations (constraints).

Action

We were given some information about the factories and customers. We define that information into parameters in our model:

Decision Variables

uijm: the number of units transported from factory i to store j in month m

Silm: the number of units produced at factory i from production line l in month m

Objective function

Our objective is minimizing the annual total cost which includes cost of production and cost of transportation. The summation of transportation cost from each factory [i] to store [j] will be the total transportation cost. The cost of production at each factory[i] for production line [l] is equal to the unit production cost [c] multiply by the total unit produced [S] at the respective factory [i] for production line[l]. There is 20% of premium charged by LM Trucking, this is reflected by the multiplication of 1.2 which is 120% of the total cost. The period is 1 year, hence summing the total cost of 12 months.

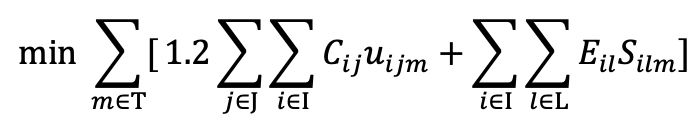
Constraints

1. Demand Fulfilment on Transportation: this constraint ensures the number of units transported from all the factory to store [j] can fulfil the demand of each store [j].

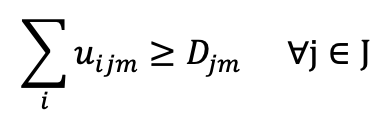
2. Production Capacity: this constraint ensures the total production for all the production lines does not exceed the production capacity of each factory [i] every month.

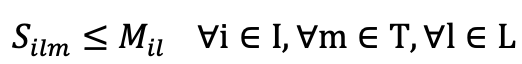
3. Demand Fulfilment on Factory: this constraint ensures the total units produced in 3 factories able to fulfil DinoBall’s monthly demand [m].

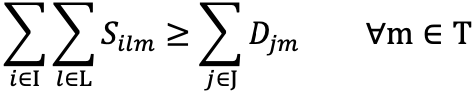
4. Transportation Units Can’t Exceed Production Units: this constraint ensures the total units transported from facility [i] to store [j] less than or equal to the total units of production at facility [i] from all the production lines [l] in month [m].

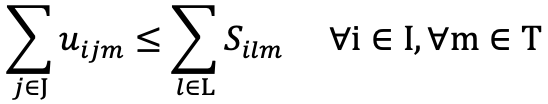
5. Consistent Production: this constraint ensures the total units transported from facility [i] to store [j] less than or equal to the total units of production at facility [i] from all the production lines [l] in month [m].

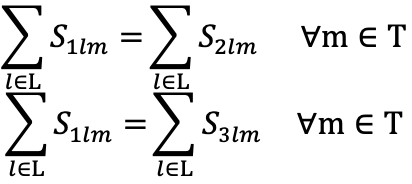
6. Equal Wear and Tear: these constraints ensure consistent wear and tear for each production line. The run time for each production line is equal to units produced by each production line divide by the rate of production of each production line.

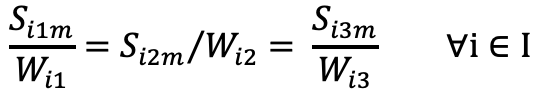
7. Non-negativity: this constraint ensures all decision variable are non-negativity.

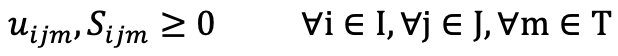
Assumptions

1. Every truck carries specific demand, but the unit transportation cost was calculated based on full capacity.
2. Fixed holding cost - Assume the holding cost for each store is known and fixed.
3. Inventory Model wasn’t considered since inventory capacity at the stores wasn’t known.
4. Each truck can only transport to one store - Assume there is no detour to another store when transporting from factory i to store j.

Result

Based on our analysis, the total cost of the original model is $2,747,837.5 and the total saving for removing constant unit production in every factory is $1,242,638. This model is recommended if the cost of restructuring the company is lower than the total saving amount from model 1. According to the analysis, “Fast Prod” production lines are capable to save $5,810,068 over three years compared to the old production lines. “Fast Prod” is highly recommended if the cost of upgrading the production lines is lower than $5,810,068. Besides, this saving has not included the salvage value of old production line. If we assume the old production lines have a total salvage value which is equal to 10% of the new production lines. The total saving would be $5,810,068 – 0.9 * Cost of Installing “Fast Prod”. The inventory model would also be recommended for lowering the cost of the model. Inventory could be potentially stored at stores where the holding cost per unit is less than the transportation cost of the unit. Also, the trucks could carry up to a full 250 units with normal optimization problem becoming a Routing and Scheduling problem.

Reference

Gurobi Jupyter notebook modeling examples. Gurobi. (2022, April 4). Retrieved May 4, 2022, from: https://www.gurobi.com/resource/modeling-examples-using-the-gurobi-python-api-in-jupyter-notebook/

Code

• Jupyter Notebook
• Python

Authors

Yu Heng Chien, Ching Ju Hsiao, Shu Nee Khor, Chia Wei Liu, Harsh Rajendra Somani

Instructor: Dr. Joseph Geunes

Texas A&M University Department of Industrail Engineering