Supply chain
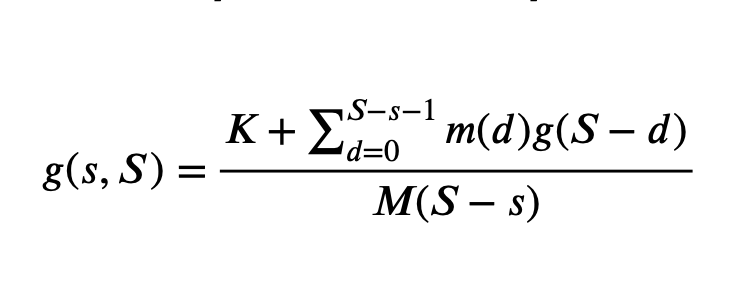
Solving Stochastic Inventory Problem: Periodic Review
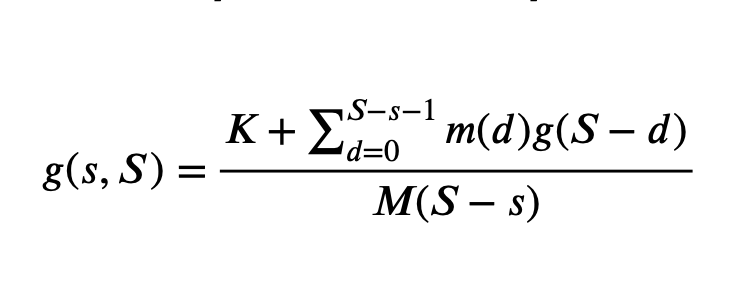
Language:
- Python: Created full algorithm for solving periofic review’s stochastic inventory problem in real life
Situation
Weekly demand for refrigerators at an appliance store has a Poisson distribution with 4. The holding and stockout cost for refrigerators at the store are $40 and $125 per week, respectively. Replenishment orders for refrigerators incur a fixed cost of $150.
Find the optimal parameters (s, S), and the corresponding optimal cost.
Solution Approach
Additionalpropertiesthathelpdeviseanalgorithm:
-
Let y* minimize g(y); then s* ≤ y* ≤ S*
- We only need to look for s≤y* and S≥y*
-
Let s = max{y < y*|g(y, S) ≤ g(y)}; then s is the optimal reorder point for S
- Given S, the biggest s smaller than y* such that the cost per period of the corresponding (s, S) policy does not exceed the single period cost at that reorder point is optimal for S
-
If S’ and S are two order-up-to levels, then g(s*(S),S) < g(s*(S’),S’) if and only if g(s*(S’),S) < g(s*(S’),S')
- Suppose we use the optimal reorder point for S’ (s*(S’)) together with some other S; if this is better than using this reorder point with S’ itself, then the best solution with S is better than the best solution with S'
-
If (s*, S*) are optimal with cost g* = g(s*, S*) then S* ≤ max{y ≥ y*|g(y) ≤ g*}
- Given a proposed (s, S), if there is a y’ ≥ y* with single-period cost g(y’) less than or equal to g(s, S) and S > y’, then (s, S) cannot be optimal
-
We can now state an algorithm for finding (s*, S*)
Algorithm
While g(S) ≤ g':
If g(s', S) < g',
Set S'=S
While g(s,S')≤g(s+1):
Sets=s+1
End while
Set s'=s;g'=g(s',S')
End if
Set S = S + 1
End while
Return (s', S')